I can show you my solution, now that the deadline has expired. Here it is.
There are two tasks this week:
No group projects for this without my authorization.
In the lab at Institut Galilée you have to use the usual small hack to add my customized paths to $PATH, so that you can use the version of Guile that I have installed in my home directory:
You have to execute the command line above in each terminal you use, before being able to execute guile.
You have already seen a solution for the problem of computing the derivative of a mathematical expression encoded as an s-expression. That solution used recursion on sub-expressions, and was structured like an interpreter. It was an example of symbolic computation, a task Lisp excels at.
This week's task is different: the parameter of the function you have to write is just a function, not a structured s-expression made of conses, symbols, numbers and the empty list. What you have to write is a higher-order function (Lisp is also a good language to work with them): your function will take another function as its parameter, and return a third function as the result. Since the parameter is a function you can essentially only apply it: you can't analyze by working inductively, because it's an atomic object.
Your function should be called derivative and must take exactly one parameter (the function the derivative of which should be computed), and return another function. derivative must work on any function taking one number (only one) and returning another number.
Think of the mathematical definition of the derivative: it involves a limit for a quantity h approaching zero. You can get a good approximation of the numeric value of the limit by using a very small positive value for h, such as 0.00001.
(derivative sin) should return a function which is an approximation of cos, and (derivative (lambda (x) (+ x 1))) should return an approximation of the constant function always returning 1.
So, if your solution is correct, ((derivative cos) 0) should return a value very close to 0 and ((derivative sin) 0) should return a value very close to 1.
You have to use guile-with-graphics for this. This task is meant to help you learn the graphic primitives needed for the big project.
Write a procedure taking two parameters, a one-argument function (just as in the task above) and a color, which plots the graph of the function on the carthesian plane using the given color.
You must also draw the carthesian axes in some way (you can even just plot two lines, for a lower bonus).
This task is not hard at all, but you should write everything cleanly, and give reasonable names to your procedures. If you don't do that then the thing will quickly become a mess (and you will get a lower bonus, too).
I strongly suggest you to write helper functions to convert from carthesian coodinates to window coordinates, and vice versa. The most "difficult" part here is the coordinate conversion.
You can use three global variables for storing the value of:
You should read and understand scm/line-demo.scm in guile-with-graphics before writing any code.
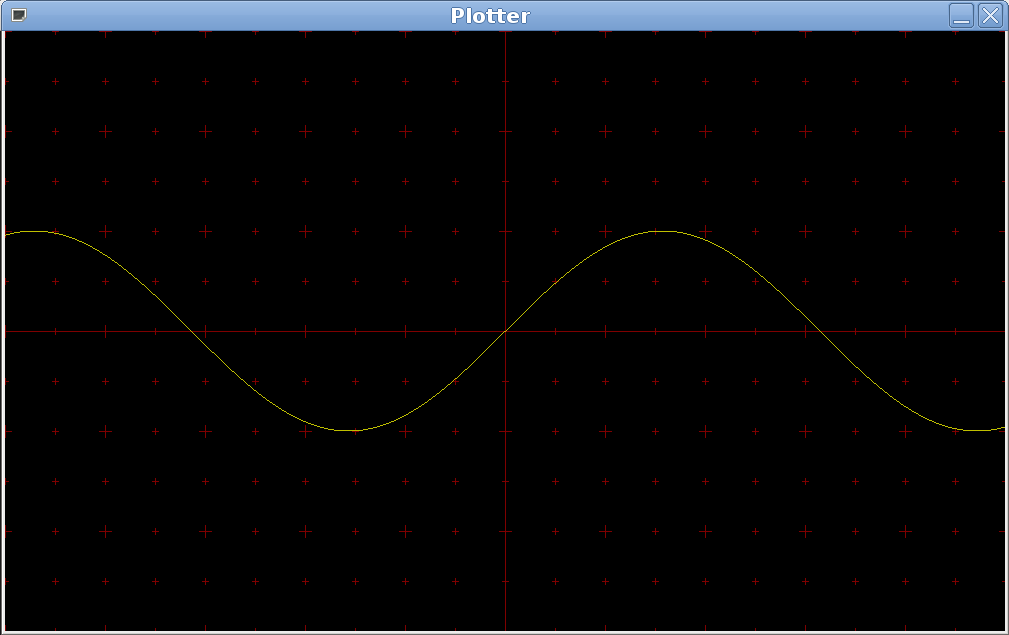
This is what I see with my solution when I draw the axes, plot the sinus function in yellow and then refresh the window:

There are many possible solutions of varying complexity and power; I will take both point of views in consideration when assigning your bonus. Pay attention to copyright and license headers.